13 décembre 2020 par Étienne Durup
Dans l’épisode 2, nous nous sommes arrêtés sur la constatation frustrante suivante : malgré l’apport incontestable d’un schéma comparatif à la même échelle de différents objets connus, l’opinion que j’essaie de me faire sur le projet d’éoliennes, et notamment la question de leur visibilité nécessite un peu de travail supplémentaire.
Plusieurs facteurs peuvent intervenir sur la vision que l’on a d’un objet dans la nature. Si on laisse de côté la qualité de la vision de la personne qui observe, on peut citer en particulier :
- la taille de l’objet (élément discuté dans notre épisode précédent, mais nous y reviendrons) ;
- la distance à laquelle il se trouve ;
- la luminosité et les contrastes de couleur ;
- les caractéristiques de l’atmosphère ;
- les obstacles.
Aujourd’hui, nous allons parler de la combinaison des points 2 et 5.
Pour commencer, nous écartons de la discussion les obstacles naturels ou non que peuvent constituer par exemple les navires ou les terres émergées en milieu marin. Nous considérons qu’aucun bateau ne vient s’interposer entre nous et l’objectif, ni aucune terre émergée et on suppose, par conséquent, qu’on n’est pas allé lâchement se fourrer de l’autre côté de l’île, quelque part entre les grands sables et le fort du Grognon.
Alors pourquoi diable, sommes-nous en train de parler d’obstacle ?
Eh bien tout simplement parce que la terre est “ronde” (il vaudrait mieux dire “sphérique” et ce serait encore faux vu qu’elle est légèrement aplatie aux pôles) ; de ce fait, à partir d’un certain moment elle constitue elle-même l’obstacle. Expliquons cela par un schéma.
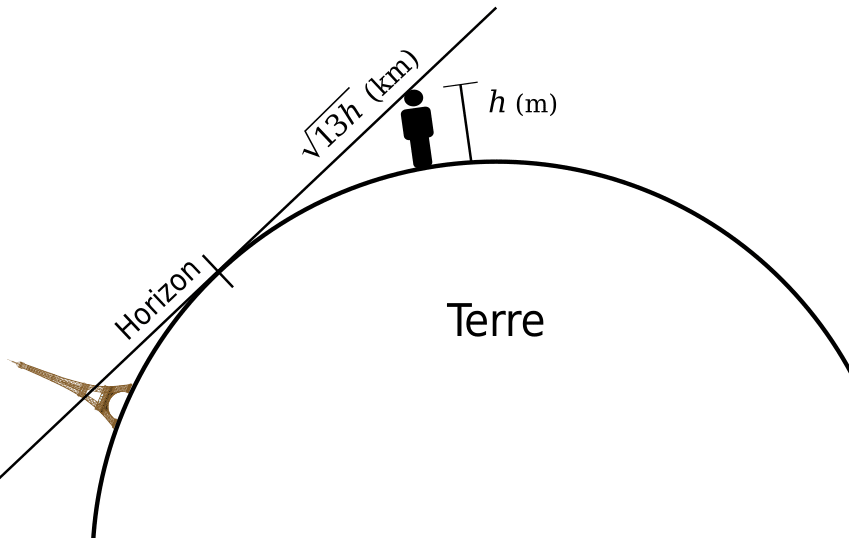
Si un objet est suffisamment loin de la personne qui l’observe, la partie basse disparaît peu à peu sous la ligne d’horizon au fur et à mesure que la distance augmente entre les deux.
Bien entendu les tailles du petit bonhomme et de la tour Eiffel sont exagérées sur ce schéma, mais il est facile de faire le calcul de la ligne d’horizon théorique d’une personne située à une hauteur donnée, dès lors qu’on connaît la taille de la personne et l’altitude à laquelle elle se trouve.
Le schéma(1) donne une formule de calcul approximative mais suffisante pour notre propos(2).
J’invite les élèves de 4e à réviser ici leur théorème de Pythagore. Ils pourront faire le calcul eux-mêmes sachant que le rayon de la terre est en moyenne de 6 371 km (eh oui, je l’ai déjà dit plus haut, la terre n’est pas parfaitement sphérique). Il devrait trouver un coefficient multiplicateur d’environ 12,74 ce qui n’est en effet pas très loin de 13 lorsqu’on sait toutes les approximations que nous pouvons nous permettre dans ces calculs (voir les prochains épisodes).
À partir de là, il devient facile de calculer la distance de l’horizon dans différentes situations. Le tableau ci-dessous en donne quelques exemples.
| Hauteur des yeux (en m) | Distance horizon (en km) |
| 1,7 | 4,7 |
| 11,7 | 12,3 |
| 21,7 | 16,8 |
| 40 | 22,8 |
| 300 | 62,4 |
Mais que devient notre tour Eiffel dans tout ça (en admettant qu’elle flotte sur l’eau) ? À partir de quel moment son extrémité passe-t-elle sous la ligne d’horizon du petit bonhomme (c’est peut-être une petite bonne femme d’ailleurs…).
Pour le savoir il suffit de lui appliquer la même méthode en calculant tout simplement la distance à la ligne d’horizon de son sommet. Faisons simple et disons qu’elle mesure 300 m. La ligne d’horizon de quelqu’un observant depuis son sommet serait donc située à environ 62 km.
Elle serait donc sous l’horizon d’une personne dont les yeux seraient à 40 m d’altitude, si cette personne était située à environ 62 + 23 km, soit environ 85 km de distance (à ce stade les centaines de mètres n’ont plus de sens).
Si elle était plus proche, la personne l’observant de loin en verrait-elle un bout qui dépasse ?
Et si elle était plus loin, est-il certain qu’on ne la verrait pas dépasser ?
Et pour nos éoliennes ?
La réponse à ces trois questions est une autre histoire, que nous aborderons dans les prochains épisodes.

